INTRODUCTION TO THE COLLATZ CONJECTURE

OEOEEOEOEOEOEOEEOEEOEOEEOEOEOEEOEOEOEOEEOEEEOEOEOEEOEOEE OEOEOEOEOEOEEEOEOEOEOEEEEOEEOEEOEEEEOEEEOEOEOEEEEEOEEEEO

For the benefit of readability, a further change consisting of the insertion of a space immediately before each O in the series breaks the series up into fragments called Syllables. The number of Syllables in a Signature is a very important factor in the analysis of the Collatz process as you will see in subsequent sections of this report.

OE OEE OE OE OE OE OEE OEE OE OEE OE OE OEE OE OE OE OEE OEEE OE OE OEE OE OEE OE OE OE OE OE OEEE OE OE OE OEEEE OEE OEE OEEEE OEEE OE OE OEEEEO

It should be noted that all Signatures and Syllables in this report begin with O, which implies that only odd numbers are of interest. This is because the application of the Collatz process to an even number immediately reveals an underlying (and smaller) odd number, so why waste time and space by retaining a letter E at the beginning of a Signature?

The following quote is extracted from the "Collatz Conjecture" entry found in Wikipedia:

If one considers only the odd numbers in the sequence generated by the Collatz process, then each odd number is on average 3/4 of the previous one.

Words to this effect can sometimes also be found in Internet articles which deal with the Collatz Conjecture, but as far as I have been able to see, it is just an observation drawn from the results of computer scans of the Collatz process. I have searched quite diligently, but unsuccessfully, for an analytical proof of the observation. It is a critical piece of information in the study of Collatz, and has a pivotal role in the next phase of this discussion. Accordingly an attempt will now be made to present two proofs which leave no doubt about its validity.

The multiplication by 3 is an integral part of every syllable, but how many divisions by 2 are there? If the average value of syllables is to be maintained at 3/4, then an Average of 2 divisions by 2 for each syllable is required.

PROOF 1 - BASED ON EMPIRICAL EVIDENCE.
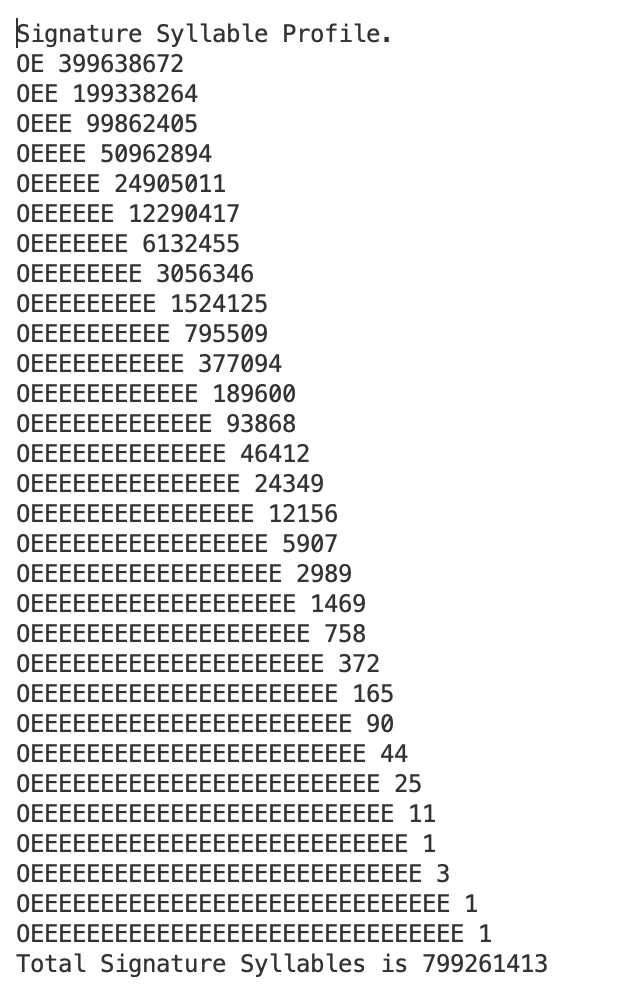
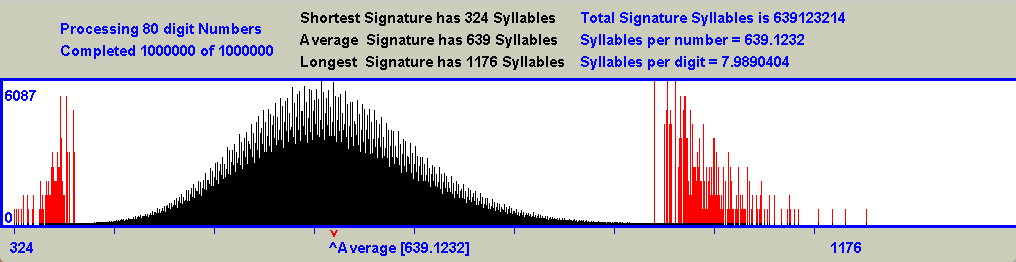
The Signature Syllable profile which follows contains the data generated by a program which submits one million randomly selected one hundred digit numbers to the collatz process, and lists the numbers of syllables encountered in Syllable length order. The following notes draw your attention to important aspects of the data:-

1. The total number of syllables encountered by the program is reported as 799,261,413 syllables.

2. Each line of the profile contains a single syllable, and includes a count of the number of times that syllable type was encountered during the process. The product of that count and the number of Es in the syllable gives us the total number of divisions by 2 performed by that syllable.

3. The calculation described in 2 above is repeated for each syllable, and accumulated into a counter.

4. When the Collatz process has completed its task, the counter reports a total of 1,598,138,736 divisions by 2.

5. Finally, we can calculate the Average number of divisions by 2 generated by each syllable (1,598,138,736 divided by 799,261,413), to give us a result of 1.9995. Clearly, we make a negligible error if we take this value to be 2.

6. And so, the final value of a syllable is the 3 by which all syllables are multiplied, as well as an Average of two division by 2, giving us a final value of 3/4. Obviously 3/4 is less than one which means that on the average each syllable will reduce the Collatz number by a factor of 3/4. The end result is inevitable. The Collatz number will gradually decrease to 1. At this point, I think we can say QED.

6. This conclusion was derived from the real world data produced by a program executing a simple algorithm for the Collatz process. It accords well with what Collatz researchers have seen happening for the last 84 years, but have failed to explain!

PROOF 2 - BASED ON LOGICAL ANALYSIS.
The appearance of each odd number in the sequence generated by the execution of any Collatz process signals the completion of the current syllable, and gives us the opportunity to assess the impact which that syllable has had on the number being processed.

To do this we need to have a clear and concise answer to the question "What effect does each Syllable have on the value of the Number being processed." To answer this question, we need to calculate the value of the Average Syllable. This is probably the most confusing section of the entire report, as it needs to take into account certain considerations involving the variable lengths of the Syllables, and also the probabilities associated with the number of divisions by two required by each of those Syllables. This calculation is important. It doesn't depend in any way on time consuming computer scans. It is derived from the simple and well understood behaviour of numbers which are subjected to a series of clearly defined arithmetic operations. The intention is to reinforce the conclusion already reached in PROOF 1.

Every Syllable begins with OE, which implies the need for:-
- A Multiplication by 3.
- An Addition of 1.
- A number of Divisions by 2 until the number becomes odd again. This could become quite a large number when you are applying the Collatz process to VERY large numbers.
The probability of there being only 1 of these divisions by 2 is 1/2.
The probability of there being 2 of these divisions by 2 is 1/4.
The probability of there being 3 of these divisions by 2 is 1/8.
The probability of there being 4 of these divisions by 2 is 1/16.
The probability of there being 5 of these divisions by 2 is 1/32.
The probability of there being 6 of these divisions by 2 is 1/64.
etc.

Clearly, the probabilities decreases by a factor of 2 for each E added to the Syllable, and so longer Syllables are progressively less likely. However they do have a greater impact on the Collatz process due to the greater number of divisions by 2. These two effects compete with each other and produce a result which you may find surprising...The Average number of divisions by two in a large group of syllables generated by the Collatz process will always be 2.

The reasoning presented above is captured in tabular form in the following:-

Signature Syllables	D(ivisions) by 2	Probability	DxP	DxP (summation)
OE	1	1 / 2	1 / 2	0.5
OEE	2	1 / 4	2 / 4	1.0
OEEE	3	1 / 8	3 / 8	1.375
OEEEE	4	1 / 16	4 / 16	1.625
OEEEEE	5	1 / 32	5 / 32	1.781
OEEEEEE	6	1 / 64	6 / 64	1.875
OEEEEEEE	7	1 / 128	7 / 128	1.93
OEEEEEEEE	8	1 / 256	8 / 256	1.961
OEEEEEEEEE	9	1 / 512	9 / 512	1.979
OEEEEEEEEEE	10	1 / 1024	10 / 1024	1.988
OEEEEEEEEEEE	11	1 / 2048	11 / 2048	1.994
OEEEEEEEEEEEE	12	1 / 4096	12 / 4096	1.997
OEEEEEEEEEEEEE	13	1 / 8192	13 / 8192	1.998
OEEEEEEEEEEEEEE	14	1 / 16384	14 / 16384	1.998
OEEEEEEEEEEEEEEE	15	1 / 32768	15 / 32768	1.998
OEEEEEEEEEEEEEEEE	16	1 / 65536	16 / 65536	1.998

About the contents of this table.

Signature Syllables.
A list of possible Signature Syllables which contain varying numbers of Es from 1 up to 16. Syllables longer than this will of course be encountered when very large numbers are submitted to the Collatz process. This would result in the table growing longer to accomodate the new numbers, but stopping at 16 will suffice to demonstrate the averaging process which occurs here. These syllables are an exact copy of those listed in the data generated by the program mentioned above.
[D]ivisions by 2.
This is simply the number of Es contained within the Syllable.
[P]robability.
The probability of a randomly selected Signature Syllable generated by the Collatz process being of this type. As you can see, each Syllable type has a probability of half that of the previous Syllable type. The sum of the probabilities in this column will approach a value of 1 as the list is extended.
[D]x[P].
The product of the number of divisions by two and the probability of this Syllable appearing. The resulting number provides a measure of the overall probability of achieving a division by 2 by means of this Syllable type when a Syllable is generated. In fact it may be treated as a small fractional part of a division by two, and may be combined together with other small fractional parts to create the required additional division by two. This may sound like an odd thing to do, but I claim that it is perfectly permissble when the end result we are seeking is an AVERAGE.
[D]x[P] (summation)
The numbers in this column provide a running total of the DxP values listed in the column headed DXP. Scanning down this list, it becomes obvious that the acccumulation of fractional parts mentioned above is increasing toward a target value of two divisions by two. So using a quite different approach, we arrive at a result identical to that obtained in PROOF 1.

Summing up then, the processing of each Signature Syllable provides one multiplication by 3 (and an addition of 1) as well as an AVERAGE of two divisions by 2. If we ignore the addition of 1, we find that each additional Signature Syllable effectively multiplies the number by a factor which is moving ever closer to 3/4. This relationship is notable, and is worthy of a title. I propose that it should be called The rule of 3/4.

It acts to reduce the size of the Number as the processing of a Collatz sequence proceeds. Admittedly circumstances are sometimes seen (and can be triggered by the use of the Signature / Number conversion algorithm) in which a Number can undergo significant degrees of growth, see Signature / Number conversion but even when such circumstances do arise, the effects are soon erased again by the normal operation of the Collatz process, and in particular by the operation of the Rule of 3/4.

It is worth stressing once again that the figure of 3/4 that we are referring to here is strictly an AVERAGE figure. Most syllables will not evaluate to 3/4. The actual value will be 3/(2ⁿ) where n is the number of consecutive Es contained within the syllable. The value of n will generally be a small number which rarely intrudes into the domain of multidigit numbers (50% of the time it will be 1).

At this point, we could reasonably claim to have proved the conjecture, but we will move on to see what other interesting results are waiting to be discovered.

THE RULE OF 8.

Now that we have confirmation of the Rule of 3/4, it's time to move on to the Rule of 8. I trust that you will be surprised and delighted by the action of this rule as it takes the notoriously erratic behavior of the Collatz process, and tames it to the point of boring predictability.

Now we know that when the Collatz function processes one Syllable of a Number, it multiplies that number by an Average of 3/4. So what will happen when the Collatz function subjects a number to a sequence of 8 Syllables. Not surprisingly, it will multiply that number by a factor of (3/4)⁸. Beware of the answer of 0.1 offered by most calculators. Calculators do indulge in a small measure of rounding and in fact the correct answer is closer to 0.10011, but for our purposes, 0.1 will do nicely.

Isn't this amazing! It means that on AVERAGE, the Number you are working on decreases by a factor of 10 each time 8 Syllables are processed. Take it one step further, and you will realize that, ON AVERAGE, a multi digit Number loses one digit each time eight Syllables of the Collatz process are processed.

This is the basis for what I call The Rule of 8 which will be demonstrated shortly. When you study this topic, I believe you will be pleasantly surprised at how closely numbers right across the infinite number spectrum obey this rule.

Three important caveats.

This Rule of 8 is only an approximation (although a truly remarkably precise one), and as a result small departures from it will be caused by the following:-

The 3 in the mathematical statement is always accompanied by the addition of 1. This is not expected to cause a big departure in the operation of the Rule, but it is always present, and the departure is always in the same direction. In any case, it is an essential part of the Collatz process as it ensures that we have an even number to restart the required chain of divisions by 2.
The 4 is the average calculated in the Rule of 3/4 analysis discussed previously. We can rely on the fact that it will be very close to 4 due to the balancing act between the increased number of divisions by 2 in some syllables, and the comparative rarity which accompanies such cases.
The mathematical statement above doesn't give us exactly one tenth, although it is, fortuitously, (you might even say serendipitously) very close to that figure. As a result, we are entitled to be quietly confident that the Rule of 8 will be closely observed.

DEMONSTRATION OF THE RULE OF 8.

It will be very much to your advantage if you have a working copy of the Collatz program on your computer as you study this section of the report. The program which supports the principles discussed in this report was generated over a period of some years while the principles themselves were emerging from my research. During this time, a program called Crossword Express was also being developed, and at the time it seemed appropriate to incorporate the much shorter Collatz program into the main body of Crossword Express. As a result, if you go the extra mile to download and install this program you will receive a significant bonus of an extensive puzzle generation platform which I believe surpasses the performance of all competing products, and it won't cost you a cent. The entire package is written in the Java programming language, and so it can be installed and run on both Apple and Windows computers. Please visit the Crossword Express web site at crauswords.com and follow the instructions to download and install a copy of the program called Crossword Express. There is no point in reading further until you have completed this step

When you have the program installed and running, Select the Collatz option from the Crossword Express menu, and follow the instructions listed below:-

To begin, select Rule of 8 Demonstration / Rule of 8 Options and set the following Options:-
Digits per Number - 30.
How many Numbers - 100000.
Bar Graph spacing - 1.
Display Bar Graph every 50 numbers.
Leave the others at their default values, but don't hesitate to experiment with them as a learning exercise.
Click Rule of 8 Demonstration to start the generation of the demonstration graph.

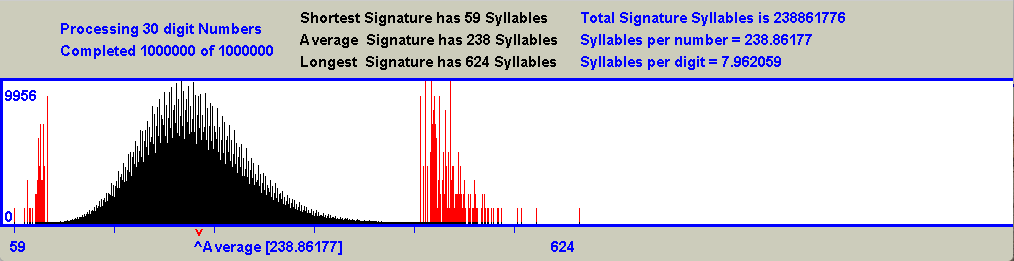
The results of this demonstration are best described by reference to the typical output shown in the following graphic:-

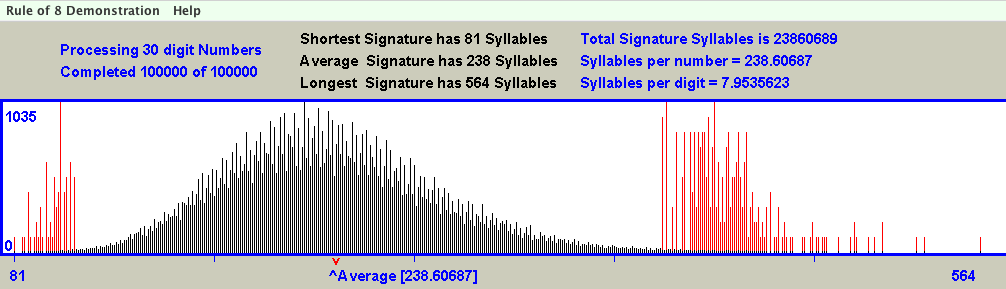
As the demonstration runs using the defaults recommended, the program applies the collatz process to one hundred thousand 30 digit numbers, and in so doing produces a set of one hundred thousand Signatures for those numbers. The important information here is not the content of the Signature, but its length. The program maintains a list of Signature lengths, and as the Signature length of each number is determined, the list item for that length is incremented by one. When all one hundred thousand numbers have been processed this list can be used to display the histogram you see in the graphic. As the program runs, it provides an indication of progress by redrawing the histogram at regular intervals. This can be quite spectacular to watch, and is recommended for your entertainment.

It is hoped that the following dot points will add meaning to what you see in the above graphic:-

The X axis of this histogram is calibrated in terms of Signature lengths which range between 81 and 564. These figures are also included in tabular form above the histogram.
The Y axis is calibrated between 0 and 1035, indicating that the most common Signature length of approx 240 was achieved by 1035 Signatures.
A downward pointing red arrow below the x axis points to the location of the expected average value of Signature Syllables predicted by the Rule of 8, and an upward pointing blue arrow labeled Average points to the location of the actual average for the numbers processed so far. It is quite entertaining to watch this indicator as the program runs. Initially it wanders up and down but quickly settles down to a number very close to the predicted value of 240
Although 81 is the shortest Signature length encountered in this particular demonstration, it would be quite wrong to assume that 81 is the shortest possible Signature for 30 digit numbers. In fact, there is always at least one, and often two numbers which will result in a Signature having only one Syllable. In the case of 30 digit numbers, the numbers 422550200076076467165567735125 and 105637550019019116791391933781 will collapse to 1 with a single Syllable Signature. These numbers look impressively large, but considerably less so when expressed as (2¹⁰⁰ - 1) / 3 and (2⁹⁸ - 1) / 3.
Similarly, although 564 was the longest Signature encountered in the demonstration, it is certainly not the longest possible Signature. Unlike the shortest Signature, finding the longest Signature seems not to be a trivial matter. This could be fertile ground for people who can't resist a mathematical challenge.
The shape of this histogram will strike a chord with anyone who has more than a passing interest in the subjects of probability and statistics. The graph is immediately recognizable as a bell curve, or "normal" distribution with some obvious differences. The main difference is that it is very far from being the smooth curve normally expected. It seems that certain Signature length values are favored by the Collatz process while others are disadvantaged. Why this is so may be another interesting question for additional research in the future.

A more detailed look at the Rule of 8 results.

Greater insights into the Rule of 8 can be obtained by running a much more ambitious test. The next graphic shows the result of running the program with one million 100 digit numbers. This means that we are testing numbers in the vicinity of 10¹⁰⁰ which is approximately the number of atoms in one hundred million trillion universes. This is obviously a very big number, but successful trials have been performed using numbers having 1,000 digits and even up to 10,000 digits. Regardless of the enormity of the numbers being tested, the results always conform very closely with the following description.

The Collatz curve for 100 digit numbers.

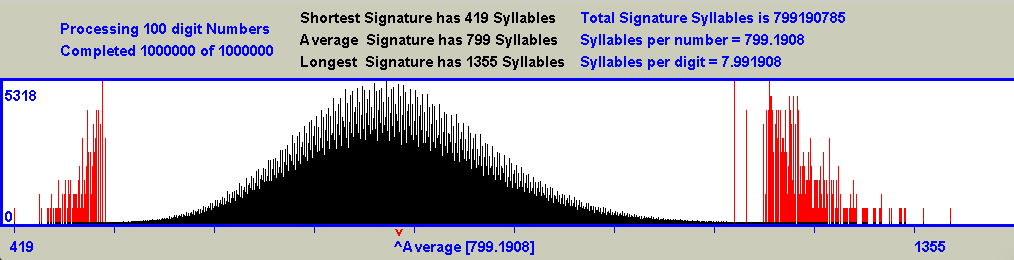
The Normal Distribution curve is again firmly in evidence with the great majority of data points in this histogram crowded very compactly around the value of 800, which is the value suggested by the Rule of 8.
The curve of the histogram thins out very substantially as it approaches both the left and the right extremes of the graphic.

A closer look at the extremes.

The tapering of the histogram at the extremes finally results in little more than a single pixel being displayed. Naturally we would like to know what is actually happening there. This is taken care of by printing the bars of the histogram in two passes. The first pass prints only the short bars ... the ones which represent Signature lengths which were achieved by 10 or less numbers. These bars are stretched so that the longest of them occupy the entire height of the graph. Also they are dawn using a distinctive colour to distinguish them from the rest of the graph. The second pass is drawn using black, and the scaling is organized so that the longest bar occupies the entire height of the graph.

The extreme left of the curve.

The thinning of the curve mentioned above continues to the left, to the extent that the last of the results shrink to only a single pixel.
The shortest recorded Signature has a length of 419. This is most certainly not the shortest possible Signature. It is mentioned elsewhere in this report that, for numbers having a given number of digits (100 in this case), there will always be at least one example of a Signature length of just one Syllable. The likelihood of encountering such a number in a run of the Rule of 8 program on 100 digit numbers is as good as zero. It is the same as the likelihood of selecting one particular atom out of 10¹⁰⁰ atoms or, to put it another way, one particular atom out of all the atoms in 100 million trillion copies of the observable universe. I venture to suggest that this is not very likely.
The stretched Signatures are drawn using red, and clearly show the continued reduction in frequency.
The Y axis of the histogram is calibrated in terms of frequency. The most frequently encountered Signature length was close to 800 (as suggested by the rule of 8), and was encountered 5318 times.

The extreme right of the curve.

The thinning of the curve also continues to the right, with the last Signature having a Syllable length of 1355. This is most certainly not the longest Signature possible for numbers having 100 digits. Finding longer Signatures than this is not such a simple matter as finding the shortest possible Signature. I personally have spent thousands of hours of computer time searching for 100 digit numbers which have Signature lengths exceeding 1500. There are potentially many such numbers, but finding them is a challenge. After all it is a matter of searching a list of 10¹⁰⁰ numbers, and this is such a vast number, that nobody will ever know just how many of them have a signature length exceeding 1500. They are few and very far between as demonstrated by the following list:-
1501 : 1925325427301238693436974716463324231743360748827222059797465213996993658480666367192272714798797665
1501 : 7200774491333522318966513865183887923813564533295043070788032954829439786486921553433708195977833007
1504 : 8981501245210358466941063069963587676629346197118428970148956094519761258248051502546615028160501531
1564 : 7987221001644153042341078535366145131744118543385943691991226902014405396825535417707018213937349053
1619 : 3600331009039113925769153746749094694696498083299979937511576902105590961849849887642985686915064485
1638 : 3361167335956235006254490886058520858196392634034320488088931462158525519487380443586390301124785383
I don't doubt that there are other 100 digit numbers with signatures longer than 1500, and probably even longer than 1638, but it would be optimistic in the extreme to expect to find one with an infinite length.
The similarities between the Collatz Curve and the Normal Distribution Curve are quite obvious, and lead us to the conclusion that the properties of the two curves may be very similar, if not identical. In fact if the Collatz Curve is subject to Standard Deviation in the same way as the Normal Distribution Curve, then we should expect there to be very few numbers (perhaps none) following 1638 in the list of numbers above. Don't forget that invalidating the Collatz Conjecture requires a Signature of infinite length.

CONCLUSIONS DRAWN FROM A COMPARISON OF THE COLLATZ CURVES

Consider the following set of Collatz curves:-

10 digit numbers.

20 digit numbers.

30 digit numbers.

40 digit numbers.

50 digit numbers.

60 digit numbers.

70 digit numbers.

80 digit numbers.

90 digit numbers.

100 digit numbers.

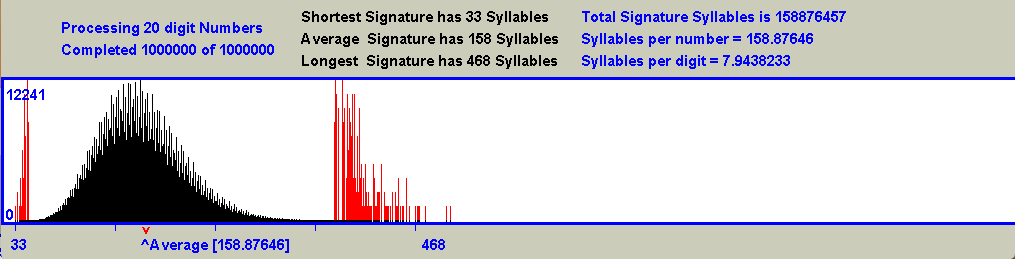
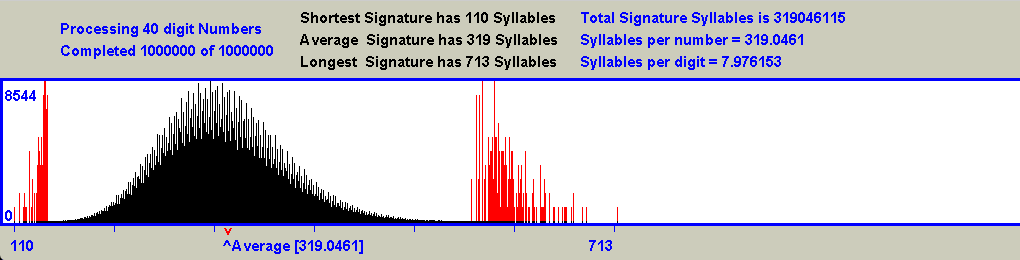
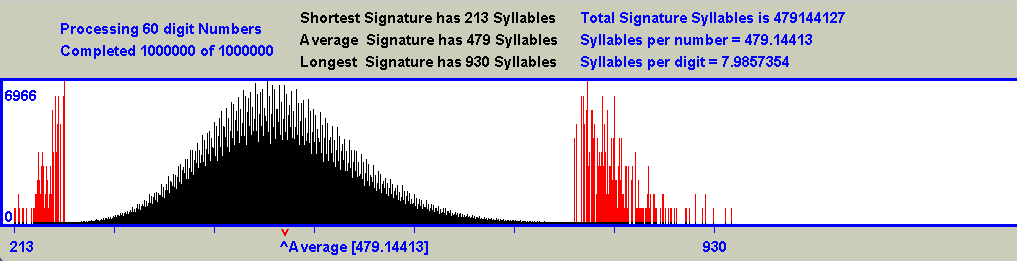
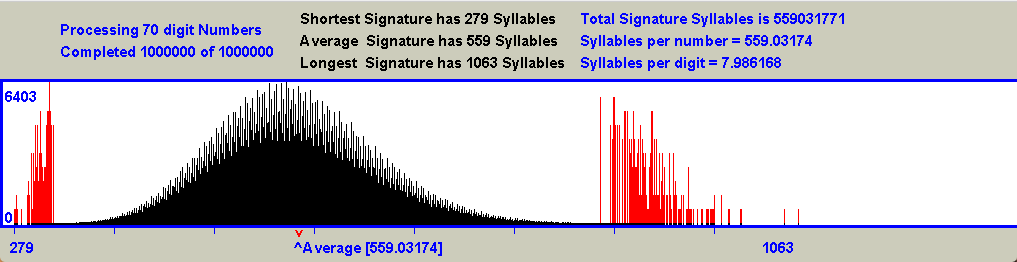
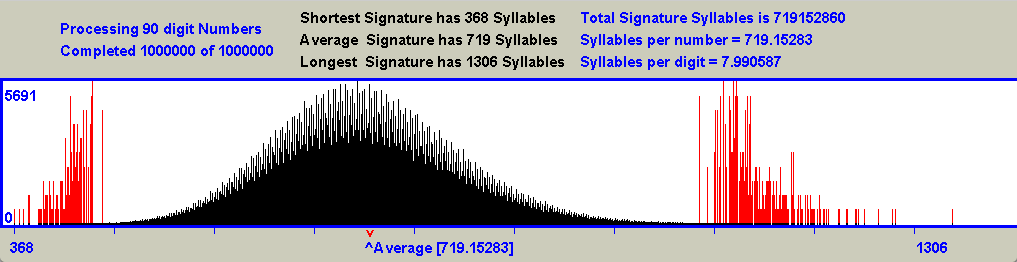
For each curve, a calculation was done to determine the ratio between the widths of the curve to the right and to the left of the point labeled 'Average'. This point is clearly not the actual central point of the curve, and the amount by which the ratio exceeds 1 provides a measure of how much wider the right portion of the curve is than the left portion. Here is the complete set of results:-

Digits	Rightmost Outlier [RO]	Center Point [CP]	([RO] - [CP]) / [CP]
10	311	80	2.888
20	468	160	1.925
30	624	240	1.6
40	713	320	1.228
50	839	400	1.098
60	930	480	0.938
70	1063	560	0.898
80	1176	640	0.838
90	1306	720	0.814
100	1355	800	0.694
1000	9692	8000	0.272

Note that the right hand portion of the curves is wider than the left hand portion, and this is more noticeable for those curves which represent numbers having fewer digits. This happens because smaller numbers have relatively longer signatures than you might otherwise expect due to the non symmetrical shape of their Collatz curves. As the length of the numbers grows, the Collatz Curves become ever more symmetrical, and the Ratio values tend towards a value of 1. For example when the curve for 1000 digit numbers was calculated (not displayed due to its size, but included in the list), the Ratio value was found to be 0.272.

This comparison sounds the death knell for any ambition to find an exception to the Collatz Conjecture. The increasing symmetry of the Collatz curve eliminates any hope of finding an infinite length signature. The shrinking right hand section of the curve is the very place where such a long signature would need to make its appearance as ever increasing length numbers are put to the test. That space is NOT going to be avaialable.

SIGNATURE TO NUMBER CONVERSION

Many advantages can be derived by shrinking the Collatz series of a number to the much more concise Signature but inevitably the need will arise for the reverse operation also to be available. This is taken care of by the Collatz Program. Please visit the Crossword Express web site at crauswords.com and follow the instructions to download and install a copy of the program called Crossword Express. The Collatz Program is a sub-program of Crossword Express.

Here are some graphics showing the results that can be obtained from the algorithm when you run the program.

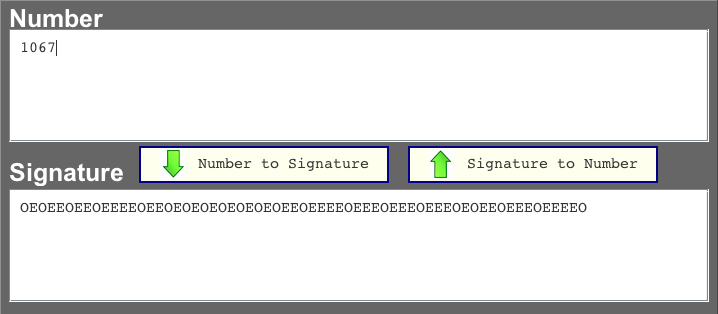
Place the Number 1067 into the Number field, and click the Number to Signature button and you will immediately see the string OEOEEOEEOEEEEOEEOEOEOEOEOEOEOEEOEEEEOEEEOEEEOEEEOEOEEOEEEOEEEEO appear in the Signature field.

Naturally you will want to check to see that the program can correctly convert this Signature back to the original Number. Click the Signature to Number button and what you will see is 8796093022208n + 1067! Is that what you expected to see? What the program generated is an infinite series of numbers each consisting of the original number 1067, plus a multiple of the number 8796093022208! Interesting? Especially when you investigate and find that 8796093022208 is an exact power of 2 namely 2⁴³.

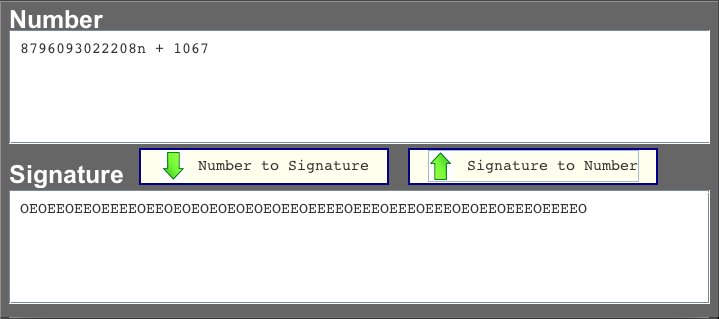
There is a third part to this window labeled Collatz Results which contains a detailed description of the steps that were taken by the algorithm as it calculated the number represented by whatever string was contained in the Signature field. It looks like this after a bit of highlighting for descriptive purposes.

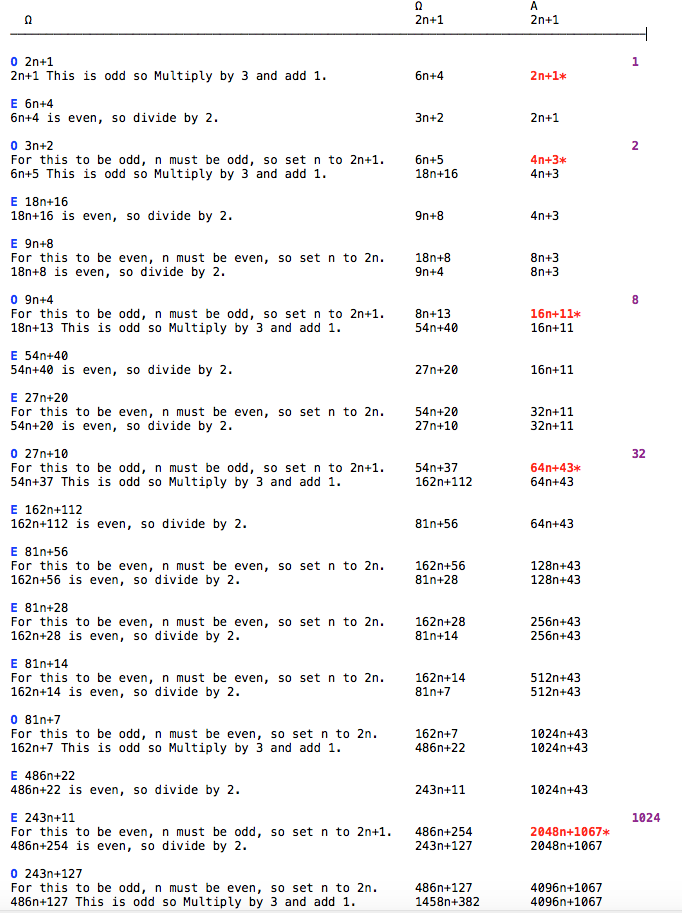
We begin with two equal odd numbers called Α (the Greek letter alpha) and Ω (the Greek letter omega). Both will be initialized to the odd number 2n+1 before processing begins. Ω will change its value as processing proceeds, as dictated by the contents of the Signature which is listed vertically in the first column. The changes to the value of Ω are effected by carefully controlled changes to the value of n. Whatever changes are made to the value of n in Ω will also be made to the value of n in Α. The result of all this will be that at the completion of the algorithm, Α will contain the required Number.

Study the highlights. The red highlights show the original number being formed in stages with each stage being the value of n used in the algorithm multiplied by a power of 2 plus a prime number. The purple numbers on the right are all powers of 2, and they equal the differences between successive red numbers. Interestingly, they represent the deconstruction of the original number into a list of ascending powers of 2. What an interesting piece of accidental numerical engineering!

Please note that the actual output of the Signature to Number algorithm is very much longer than shown here. It only includes that part of the output in which the reconstituted Number makes its appearance.

A SHORT TUTORIAL ON SIGNATURE TO NUMBER CONVERSION

This is a very short tutorial containing only two items at this stage. There is potential for many new and intriguing items to be added in the future.

Shorter than expected Signatures.

Consider the 25 digit number 2149199407454443676194133. At first sight, it appears to be a number of much more than usual length, but when you generate its Signature you will find that it contains just two Syllables :

OEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEE
and
OEEEEEEEEEEEEEEEEEEEE.

As you might expect this number was very carefully selected. Such numbers are not particularly common, but they can very easily be discovered using the Signature / Number Conversion program. Simply create a new Signature by joining the two Syllables above and typing the result into the Signature field of the Signature / Number Conversion program. Then click the Signature to Number button. The number 2149199407454443676194133 will appear in the Number field. Naturally, you can restore the original Syllable by clicking the Number / Signature button.

Longer than expected Signatures:

Now here is a very large Number, also very carefully selected, and having 3,011 digits.

199506311688075838488374216268358508382349683188619245485200894985294
388302219466319199616840361945978993311294232091242715564913494137811
175937859320963239578557300467937945267652465512660598955205500869181
933115425086084606181046855090748660896248880904898948380092539416332
578506215683094739025569123880652250966438744410467598716269854532228
685381616943157756296407628368807607322285350916414761839563814589694
638994108409605362678210646214273333940365255656495306031426802349694
003359343166514592977732796657756061725820314079941981796073782456837
622800373028854872519008344645814546505579296014148339216157345881392
570953797691192778008269577356744441230620187578363255027283237892707
103738028663930314281332414016241956716905740614196543423246388012488
561473052074319922596117962501309928602417083408076059323201612684922
884962558413128440615367389514871142563151110897455142033138202029316
409575964647560104058458415660720449628670165150619206310041864222759
086709005746064178569519114560550682512504060075198422618980592371180
544447880729063952425483392219827074044731623767608466130337787060398
034131971334936546227005631699374555082417809728109832913144035718775
247685098572769379264332215993998768866608083688378380276432827751722
736575727447841122943897338108616074232532919748131201976041782819656
974758981645312584341359598627841301281854062834766490886905210475808
826158239619857701224070443305830758690393196046034049731565832086721
059133009037528234155397453943977152574552905102123109473216107534748
257407752739863482984983407569379556466386218745694992790165721037013
644331358172143117913982229838458473344402709641828510050729277483645
505786345011008529878123894739286995408343461588070439591189858151457
791771436196987281314594837832020814749821718580113890712282509058268
174362205774759214176537156877256149045829049924610286300815355833081
301019876758562343435389554091756234008448875261626435686488335194637
203772932400944562469232543504006780272738377553764067268986362410374
914109667185570507590981002467898801782719259533812824219540283027594
084489550146766683896979968862416363133763939033734558014076367418777
110553842257394991101864682196965816514851304942223699477147630691554
682176828762003627772577237813653316111968112807926694818872012986436
607685516398605346022978715575179473852463694469230878942659482170080
511203223654962881690357391213683383935917564187338505109702716139154
395909915981546544173363116569360311222499379699992267817323580231118
626445752991357581750081998392362846152498810889602322443621737716180
863570154684840586223297928538756234865564405369626220189635710288123
615675125433383032700290976686505685571575055167275188991941297113376
901499161813151715440077286505731895574509203301853048471138183154073
240533190384620840364217637039115506397890007428536721962809034779745
333204683687958685802379522186291200807428195513179481576244482985184
615097048880272747215746881315947504097321150804981904558034168269497
87141316063210686391511681774304792596709375

According to the Rule-of-8 you might expect its Signature to have a little more than 24,000 Syllables. I won't reproduce that Signature here because it is rather large. If you really want to see it you can easily generate it using the Number / Signature function of the Collatz program.

It has 48,126 Signature Syllables which is close to twice the predicted value. So what is going on here?

If you do generate this Signature, and if you scroll to the top of the Signature Area you will find that the first 20,000 characters consist of 10,000 Signature Syllables of OE! Each of these Syllables will increase the subject number by a factor of 3/2. This will produce a number having many more digits than 3,011, and will therefore require many more than the initial 24,000 Syllables plus the additional 10,000 before it begins the normal task of processing its way down the series to the ultimate result of 1.

Needless to say, such numbers are exceedingly rare. If you were performing the Collatz process on it manually, then after a few hundred OE Syllables have appeared you could be forgiven for thinking that you had discovered the holy grail of a number that would continue increasing forever. Unfortunately you would be disappointed after 10,000 OEs had appeared. Beyond that point, the Signature will revert to form and bear all the hallmarks of a totally random process.

You can be fairly certain that you will never find such a number by accident, but using the Signature / Number conversion program makes anything possible.

There is a never ending supply of interesting experiments you can try with with the Signature to Number conversion program. It should teach you not to spend a lot of time looking for recurring patterns in the Collatz series. You can create an infinite number of Signatures, each having its own unique infinite array of numbers. In other words, you can be sure that any interesting pattern that you do find will be repeated over and over again, ad infinitum.

LIMITS TO GROWTH IN THE COLLATZ SERIES

Some commentators on the subject of the Collatz Conjecture suggest (without evidence) the possibility of numbers which grow without limit when subjected to the Collatz process. This claim really needs to be investigated.

Consider the number 2ⁿ-1
Clearly it is an odd number so, to subject it to the Collatz test, we must do the following:-
Multiply by 3 :- 3¹ * (2ⁿ - 1) = 3¹ * 2ⁿ - 3
Add 1:- 3¹ * 2ⁿ - 3 + 1 = 3¹ * 2ⁿ - 2
Divide by 2:- (3¹ * 2ⁿ - 2) / 2 = 3¹ * 2^n-1 - 1

Repeat the iteration with 3¹ * 2^n-1 - 1
Multiply by 3:- 3 * (3¹ * 2^n-1 - 1) = 3² * 2^n-1 - 3
Add 1:- 3² * 2^n-1 - 3 + 1 = 3² * 2^n-1 - 2
Divide by 2:- (3² * 2^n-1 - 2) / 2 = 3² * 2^n-2 - 1

Repeat the iteration with 3² * 2^n-2 - 1
Multiply by 3:- 3 * (3² * 2^n-2 - 1) = 3³ * 2^n-2 - 3
Add 1:- 3³ * 2^n-2 - 3 + 1 = 3³ * 2^n-2 - 2
Divide by 2:- (3³ * 2^n-2 - 2 / 2) = 3³ * 2^n-3 - 1

Even after only three iterations, the behaviour has become quite clear. At each iteration, the exponent of 3 increases by 1, and the exponent of 2 decreases by 1, and there is no reason to doubt that this state of affairs will continue indefinitely. We would have found a number which increases forever. However, a profound change will take place if the character n is replaced by a number ... say 10. Here is the list of numbers which results:-

1 1023 4 3455 7 11663 10 39365
2 1535 5 5183 8 17495 11 59048
3 2303 6 7775 9 26243

Each number is larger than the one which preceded it, and they are all odd numbers except the last! So, we can make this behaviour last for as long as we like by choosing ever larger numbers to replace n, but we can't make it last forever, as that would require n to be infinite. Anyone who makes the aforementioned suggestion will need to find another recipe for a number which behaves in the manner they have in mind. The question is, can they actually do that?

THE COLLATZ TREE

Most discussion papers dealing with the Collatz Conjecture will include some form of graphical representation of the collatz numbers. This tutorial will be no exception as it introduces the Collatz Tree. Now the Collatz Tree is infinite in extent and so only a very small portion near the base of the tree will be shown here.

^^^
65536 : 21845	43690 - 87380 - 174760 - 349520 - 699040 - 1398080 - 2796160 - 5,592,320 - 11,184,640 >>> [14563] [58253] [233013] [932053] [3,728,213]
^ 32768 ^	Sterile
16384 : 5461	10922 - 21844 - 43688 - 87376 - 174752 - 349504 - 699008 - 1,398,016 - 2,796,032 >>> [7281] [29125] [116501] [466,005] >>>
^ 8192 ^	Sterile
4096 : 1365	2730 - 5460 - 10920 - 21840 - 43680 - 87360 - 174720 - 349440 - 698,880 - 1,397,760 >>>
^ 2048 ^	Sterile
1024 : 341	682 - 1364 - 2728 - 5456 - 10912 - 21824 - 43648 - 87296 - 174,592 - 349,184 >>> [227] [909] [3637] [14549] [58,197] >>>
^ 512 ^	Sterile
256 : 85	170 - 340 - 680 - 1360 - 2720 - 5440 - 10880 - 21760 - 43,520 - 87,040 - 174,080 >>> [113] [453] [1813] [7253] [29,013] >>>
^ 128 ^	Sterile
64 : 21	42 - 84 - 168 - 336 - 672 - 1344 - 2688 - 5376 - 10752 - 21504 - 43,008 - 86,016 >>>
^ 32 ^	Sterile
16 : 5	10 - 20 - 40 - 80 - 160 - 320 - 640 - 1280 - 2560 - 5120 - 10240 - 20,480 - 40,960 >>> [3] [13] [53] [213] [853] [3,413] [13,653]
^ 8 ^	Sterile
4---- \| \| 2 \| \| \| 1 >--

Collatz Tree Essentials.

The fundamental component of any tree is the trunk. This is the the light brown section to the left of the table. It is made up of the root of the tree (the eternal loop of 1, 2 and 4) plus the continuation of the list of powers of 2 which extends to infinity. Being powers of 2, they will be either 1 mod 3 or 2 mod 3. Those that are 1 mod 3 are distinguished by the attachment of a second number which is (power of 2 minus 1) divided by 3. This number can be looked upon as a bud which will develop into a branch consisting of a series of numbers which are the value of the bud multiplied by consecutive powers of 2. Those that are 2 mod 3 cannot give rise to a branch and are therefore labeled Sterile.
Three variants in the structure of a branch can be identified:-
- If the value of the bud is 2 mod 3 (such as 5, 341 and 21845) then the values on the branch will alternate between 1 mod 3 and 2 mod 3 with the first candidate number being 1 mod 3. These branches are colored light blue in the diagram. All of the 1 mod 3 candidates are buds which will spawn another new generation of branches.
- If the value of the bud is 1 mod 3 (such as 85 and 5461) then the values on the branch will alternate between 1 mod 3 and 2 mod 3 with the first candidate number being 2 mod 3. These branches are colored lime green in the diagram. Once again, all of the 1 mod 3 candidates are buds which will spawn another new generation of branches.
- If the value of the bud is 0 mod 3 (such as 21 and 1365) then the values on the branch will also be 0 mod 3 and cannot promote a new branch. These branches are colored pink in the diagram. It would be appropriate to classify them as sterile branches.
The trunk is classified as a level 1 branch. Every other branch in the tree will have a level number which is one more than the level number of the branch from which it arose.
Every number in the tree is guaranteed to converge onto 1 when it undergoes the Collitz process, but does every natural number actually appear on the tree. I invite you to consider the conundrum as to just what characteristics would a number need to have for it not to be included on this tree.
There is a very intimate connection between the structure of the Collatz Tree and the Collatz Signature discussed at Introducing Signatures and Syllables. This is illustrated by the number 4970949 whose Collatz Signature and Collatz series are tabulated as follows:-

The Anatomy of a Signature.

O E E E E	4970949 14912848 7456424 3728212 1864106	Third level Branch. The first Syllable of the Signature of 4970949 is shown here. It originates in a level 3 branch which is external to that part of the collatz Tree shown previously and connects with a level 2 branch at the bottom right corner where it meets the odd number 932053. Any Syllable will always be contained entirely within a single branch, and will end at the point where that branch connects with the next (lower level) branch.
O E E E E E E E	932053 2796160 1398080 699040 349520 174760 87380 43690	Second level Branch. Like all Syllables, the second one begins with an odd number which must be multiplied by 3, and have 1 added to it giving 2796160. A series of divisions by 2 eventually leads us to another odd number 21845 which is the beginning of the next Syllable, located in the only level 1 branch (trunk) of the tree.
O E E E E E E E E E E E E E E E E	21845 65536 32768 16384 8192 4096 2048 1024 512 256 128 64 32 6 8 4 2	First level Branch. Here we have the third and final Syllable of our original starting number. Its initial (odd) number is 21845, which becomes 65536 after multiplication by 3 and the addition of 1. Now this number happens to be an integral power of 2, and so again we see another series of divisions by 2 which brings us inevitably to the terminating point of 1. These discussions have stressed the fact that every Syllable begins with an odd number. This is important. It is even more important to remember that EVERY odd number heralds the beginning of another branch, and that every branch is infinite in extent, having an infinite number of even numbers, one half of which will equal 1 mod 3 and so will spawn yet more new branches. This Signature is rather short with only 3 Syllables. Elsewhere in this discussion, you will encounter Signatures having vastly more than this. In fact there is no upper limit to the number of Syllables a Signature can have.
O	1	Zero level Branch. This is the absolute base of the tree and could quite reasonably be referred to as the root.

A practical example of a Signature traversing the tree.

The Collatz Tree is a vast and complex structure, and the path taken by a Signature on its journey through the tree is virtually impossible to visualize. What follows is an attempt to depict the path taken by the number 79 as it makes this journey. It is a very cut down version of the tree, and shows only those branches which were actually used.

                                ^^^^^            ^^^^      ^^^

                                19456            8608      952

                                 9728            4304      476

                                 4864            2152      238 79 158 316 672 1344 >

                                 2432            1076      119

                           ^^^^  1216             538  179    358 716 1432 2864 5728 11456 >

                           5632   608              269

                           2816   304   101   202   404   808    1616 3232 6464 12928 25856 51712 >

                           1408   152

                     ^^^^   704    76

                     3328   352    38

                     1664   176    19

                      832    88   29   58 116 232 464 928 1856 3712 >

           ^^^        416    44

           512        208    22

           256        104    11

           128             52 17   34 68 136 272 544 1088 2176 >

            64            26

            32            13 

            16 5  10   20   40 80 160 320 640 1280 2560 >

             8

             4

             2

             1

The numbers which constitute the path are colored red and blue. The color changes at the beginning of each Branch of the tree. Note that the first number of each Branch is an odd number which is the bud of that branch.
The black numbers provide extensions to each branch. All of these numbers are powers of 2 multiplied by the value of the bud of the branch.
The UP and RIGHT arrows remind you that all of these branches extend onward forever.
Remember that when an odd number is encountered, the next number (multiply by 3 and add 1) will be an even number and will be located on a branch which is one level lower than the current branch.
You will note that the path uses only a small portion of each branch located near the beginning of the branch. Naturally this won't always be the case, but Signatures which use large sections of a single branch will be something of a rarity.